重量とバランスポイントとスイングウェイトの関係

ラケットの重量とバランスポイントとスイングウェイトの関係

以下の図はラケットの重量配分を示したもので、かなり極端にしてありますが、黒丸部分に重量があります。
そして、①と②では、重量とバランスポイントについては同じになります。
それに対して、①と②の右端を持って振り回比べると、スイングウェイトは①が②の倍の数値になります。
これは、【質量×距離の二乗】がスイングウェイトの計算式だからです。

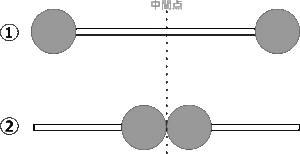
黒丸の質量を【１】、中間点までの距離を【５】とすると
①の右端の黒丸は【質量＝１】×【距離＝０の二乗】⇒スイングウェイト＝０となり、
①の左端の黒丸は【質量＝１】×【距離＝１０の二乗】⇒スイングウェイト＝１００となり、合計で１００です。
②の場合は、中間点の黒丸２個は【質量＝２】×【距離＝５の二乗】⇒スイングウェイト＝５０となります。

重量とバランスポイントが同じでもスイングウェイトは倍の違いが発生するということです。

上記の図は実際にはあり得ない重量配分ですが、下の図は実際に起こり得るケースです。

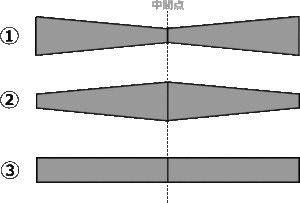
①は重量の配分が端に寄っているケース
②は重量が中央部分に寄っているケース
③は重量配分の片寄りがなく平均的に分散しているケース
この３パターンの重量とバランスポイントが同じだとしても、スイングウェイトの大きさは以下の順序になります。
①＞③＞②

昔々、プリンスで「トリプルスレットシリーズ」というのが発売されて、フレームのフェース上部２箇所とグリップに重点的に重量を配分したラケットが登場しました。
ちょうど①のような重量配分だったわけです。
その結果、重量とバランスポイントは従来モデルとそれほど変わらないのに、スイングウェイトだけがやたら重いラケットに仕上がってしまったという昔話がありました。

また、これとは逆に、①のタイプのラケットを③のような重量配分に変えると、重量とバランスポイントは変わらないのにスイングウェイトだけが軽くなるという現象が起きます。

重量とバランスポイントではスイングウェイトは確定しないという説明でした。